Sử dụng hai hàm mục tiêu trong việc giải các bài toán thuộc dạng bài toán cái túi

Trong quá trình giải các bài toán thuộc dạng bài toán cái túi, ta thấy có những bộ dữ liệu vào khi giải sẽ cho ra nhiều phương án khác nhau (nhiều đáp số), với thuật toán cái túi mà chúng ta đã được biết, sẽ chỉ đưa ra một trong số các phương án đó (có thể chưa tối ưu nhất). Trong bài viết này, tôi sẽ trình bày cách thêm một số câu lệnh vào thuật toán cái túi để giúp ta có thể chọn ra được một kết quả tốt nhất trong các kết quả tốt nhất mà thuật toán cái túi đã tìm ra.

I. Đặt vấn đề

Bài toán cái túi là một trong những bài toán điển hình khi học về phương pháp quy hoạch động. Ngoài ra, thuật toán cái túi còn được ứng dụng nhiều trong thực tiễn như: Lập kế hoạch sản xuất theo đơn đặt hàng

Lựa chọn quảng cáo trong phát thanh và truyền hình

Lựa chọn các nút mạng di động

Quản lí tài nguyên trong phần mềm,…

Với những bài toán trên, khi ứng với một bộ dữ liệu vào nào đó mà kết quả ra có nhiều phương án lựa chọn thì thuật toán cái túi chưa chọn ra được một phương án tốt nhất trong các phương án đã tìm ra. Ta xét ví dụ sau:

Một nhà máy nhận sản xuất các đồ gia dụng theo đơn đặt hàng. Giả sử trong một buổi làm việc nào đó kéo dài từ 7h đến 11h (240 phút) có đến N đơn đặt hàng. Khi sản xuất 1 đồ gia dụng thì cần 1 thời gian x và nhận được số tiền là y. Bài toán đặt ra là cần chọn những đơn hàng nào để nhà máy có thể thu về được số tiền là lớn nhất mà không vượt quá thời gian cho phép (ở đây là 240 phút). Trong trường hợp có nhiều phương án lựa chọn để thu về được cùng số tiền là lớn nhất thì thực tế con người lại muốn chọn ra được một phương án có tổng thời gian là ít nhất nhằm giảm sức lao động cho các công nhân đứng máy, giảm điện năng vận hành sản xuất… => Tiết kiệm chi phí, sức lực…

Từ những điều đã nói ở trên, tôi chọn đề tài: “Sử dụng 2 hàm mục tiêu trong việc giải các bài toán thuộc dạng bài toán cái túi” nhằm tối ưu hơn nữa trong việc giải các bài toán dạng này.

II. Nội dụng

Trước hết, ta xét bài toán sau:

Bài 1: Bài toán cái túi 2 (mở rộng)

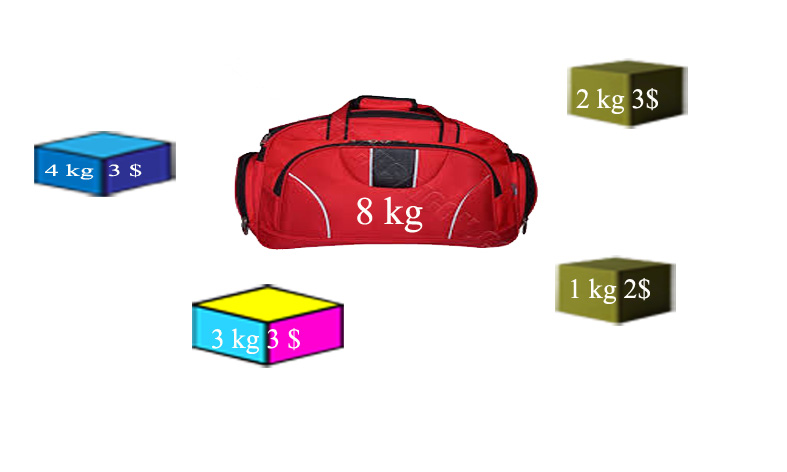
Trong siêu thị có n đồ vật (n≤1000), đồ vật thứ i có trọng lượng là i ≤10­00 và giá trị i ≤1000. Một tên trộm đột nhập vào siêu thị, tên trộm mang theo một cái túi có thể mang được tối đa trọng lượng M (M≤1000). Hỏi tên trộm sẽ lấy đi những đồ vật nào để được tổng giá trị lớn nhất (trong trường hợp nếu có nhiều phương án đúng thì ghi ra phương án có tổng trọng lượng các đồ vật được chọn là bé nhất)

Giải quyết bài toán trong các trường hợp sau:

• Mỗi vật chỉ được chọn một lần.

InputData: file văn bản bagEF.inp

• Dòng 1: n, M cách nhau ít nhất một dấu cách

• n dòng tiếp theo: Mỗi dòng gồm 2 số nguyên dương W_i, V_i, thể hiện trọng lượng và giá trị của đồ vật thứ i.

OutputData: file văn bản bagEF.out:

+ Dòng 1: Gồm 2 số, ghi tổng trọng lượng các đồ vật được chọn và ghi giá trị lớn nhất tên trộm có thể lấy

+ Dòng 2 : ghi chỉ số những đồ vật được chọn tương ứng

Ví dụ:

(Phương án: Việc chọn các đồ vật thứ 1 2 4 cũng có tổng giá trị lớn nhất là 8 nhưng tổng trọng lượng mà các vật được chọn khi đó là 8 => chưa thỏa mãn yêu cầu thứ 2 của đề bài)

* Ý tưởng

Do yêu cầu nếu có nhiều phương án đúng thì ghi ra phương án có tổng trọng lượng các đồ vật được chọn là bé nhất nên ở đây ta sẽ sử dụng 2 hàm mục tiêu F[i][j] và E[i][j]. Hàm F[i][j] được dùng để chọn ra được các đồ vật trong n đồ vật có tổng giá trị là lớn nhất mà không vượt quá trọng lượng M. Còn hàm E[i][j] thì phụ thuộc vào hàm F[i][j], nghĩa là khi mà việc chọn đồ vật thứ i hay không chọn đồ vật thứ i thì giá trị của hàm F[i][j] vẫn không thay đổi thì lúc đó mới xét tới hàm E[i][j] và nếu đồ vật thứ i thỏa mãn cả 2 điều kiện sau thì đồ vật đó sẽ được chọn

Để áp dụng chính xác các công thức của thuật toán (Cái túi), trước hết ta có thể  khởi tạo giá trị ban đầu cho bảng phương án như sau:

- Với hàm mục tiêu F: + fill(F[0], F[0]+nmax*nmax, 0);

- Với hàm mục tiêu E: + fill(E[0], E[0]+nmax*nmax, mmax+1);

          +   for (j=1;j<=m;j++) E[0][j]=0;// Các phần tử ở hàng 0 đều nhận giá trị 0

          +   for (i=0; i<=n; i++) E[i][0]=0;// Các phần tử ở cột 0 đều nhận giá trị 0

* Chương trình cài đặt cho bài toán cái túi sử dụng 2 hàm mục tiêu như sau:

// Tên tệp chương trình: BagEF.cpp

#include

#include

using std::string;

using namespace std;

const int mmax=1000,nmax=1000;

int v[nmax],w[nmax];

int E[nmax][nmax],F[nmax][nmax];

int n,m,i,j;  string s="";

void inkq()

{    cout<

    while (n!=0) { //Truy vet tu hang n lên hang 0

        if (F[n][m] != F[n-1][m]) {

            s=to_string(n) + " "+s ;    m=m - w[n];

//Da chon gói thu n roi thì chi có the mang them duoc P: M - W[n] nua thoi

        }

        else if ((E[n][m] != E[n-1][m]) and (F[n][m] == F[n-1][m])) {

            s=to_string(n) + " "+s ;    m=m - w[n];

        }

        n--;

    }

    cout<

    }

int main()

{

    freopen("bagEF.inp","r",stdin);

    freopen("bagEF.out","w",stdout);

    cin>>n>>m;

    for (i=1;i<=n;i++)  cin>>w[i]>>v[i];

    fill(F[0], F[0]+nmax*nmax, 0);

    fill(E[0],E[0]+nmax*nmax, mmax+1);

    for (j=1;j<=m;j++)  E[0][j]=0;

    for (i=0;i<=n;i++)  E[i][0]=0;

    for (i=1;i<=n;i++)

        for (j=1;j<=m;j++)

        {

            F[i][j]=F[i-1][j];

            E[i][j]=E[i-1][j];

            if ((w[i]<=j) and (F[i-1][j-w[i]] + v[i] > F[i][j]))

            {

                F[i][j]=F[i-1][j-w[i]] + v[i];

                E[i][j]=E[i-1][j-w[i]] + w[i];

            }

            else if ((w[i]<=j ) and (E[i-1][j-w[i]] + w[i] < E[i][j])

                and (F[i-1][j-w[i]] + v[i] == F[i][j]))

                   E[i][j]=E[i-1][j-w[i]] + w[i];

        }

    inkq();

    return 0;

}

- Các bạn có thể xem thêm bảng phương án dưới đây để biết vì sao các phần tử ở hàng 0 và cột 0 trong mảng E ban đầu cần gán giá trị bằng 0 ; Ở bảng dưới, trong cùng 1 ô, giá trị phía trên thể hiện tổng giá trị của hàm  F[i][j], giá trị phía dưới thể hiện tổng trọng lượng của hàm E[i][j]

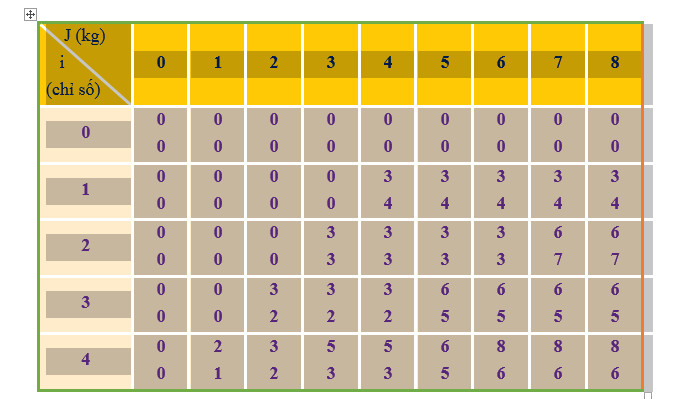
- Tiếp theo, ta tìm hiểu sự thay đổi giá trị (ở một số ô) trong bảng các phương án:

+ Ô [1,4]: 2 giá trị tại ô này đều được tính từ 1 ô [0,0]

                   F₁₄  = F₀₀ + V₁ = 0 + 3 = 3

                   E₁₄  = E₀₀ + W₁ = 0 + 4 = 4

+ Ô [2,3]: 2 giá trị tại ô này  đều được tính từ 1 ô [1,0]

                   F₂₃  = F₁₀ + V₂ = 0 + 3 = 3

                   E₂₃ = E₁₀ + W₂ = 0 + 3 = 3

+ còn tại ô [2,4]:

                   F₂₄  = F₁₄  = 3 (được tính từ  ô [1,4])

                   E₂₄ = E₁₁ + W₂ = 0 + 3 = 3 (được tính từ  ô [1,1])

+ tại ô [3,7]:

                   F₃₇  = F₂₇  = 6 (được tính từ  ô [2,7])

                   E₃₇ = E₂₅ + W₃ = 3 + 2 = 5 (được tính từ  ô [2,5])

Để tiện so sánh, dưới đây là thuật toán của bài toán cái túi mà chúng ta đã biết trước đây (chỉ sử dụng 1 hàm mục tiêu F)

// Tên tệp chương trình: BagF.cpp

#include

#include

using std::string;

using namespace std;

const int mmax=1000,nmax=1000;

int v[nmax],w[nmax];

int F[nmax][nmax];

int n,m,i,j,sum=0;

string s="";

void inkq()

{

     j=F[n][m];

    while (n!=0) { //Truy vet tu hang n lên hang 0

        if (F[n][m] !=F[n-1][m]) {

            s=to_string(n)+" "+s;//cout<

            m=m-w[n];  sum=sum+w[n];

//Da chon gói thu n roi thì chi có the mang them duoc P: M - W[n] nua thoi

        }

        n--;

    }

    cout<

    }

int main()

{

    freopen("bagEF.inp" , "r", stdin);

    freopen("bagF.out", "w", stdout);

    cin>>n>>m;

    for (i=1;i<=n;i++)  cin>>w[i]>>v[i];

    fill(F[0],F[0]+nmax*nmax,0);

        for (i=1;i<=n;i++)

        for (j=1;j<=m;j++)

        {

            F[i][j]=F[i-1][j];

            if ((w[i]<=j) and (F[i-1][j-w[i]]+v[i]>F[i][j]))

                F[i][j]=F[i-1][j-w[i]]+v[i];

        }

    inkq();

    return 0;

}

(khi chạy cùng bộ dữ liệu trên sẽ cho kết quả như sau:)

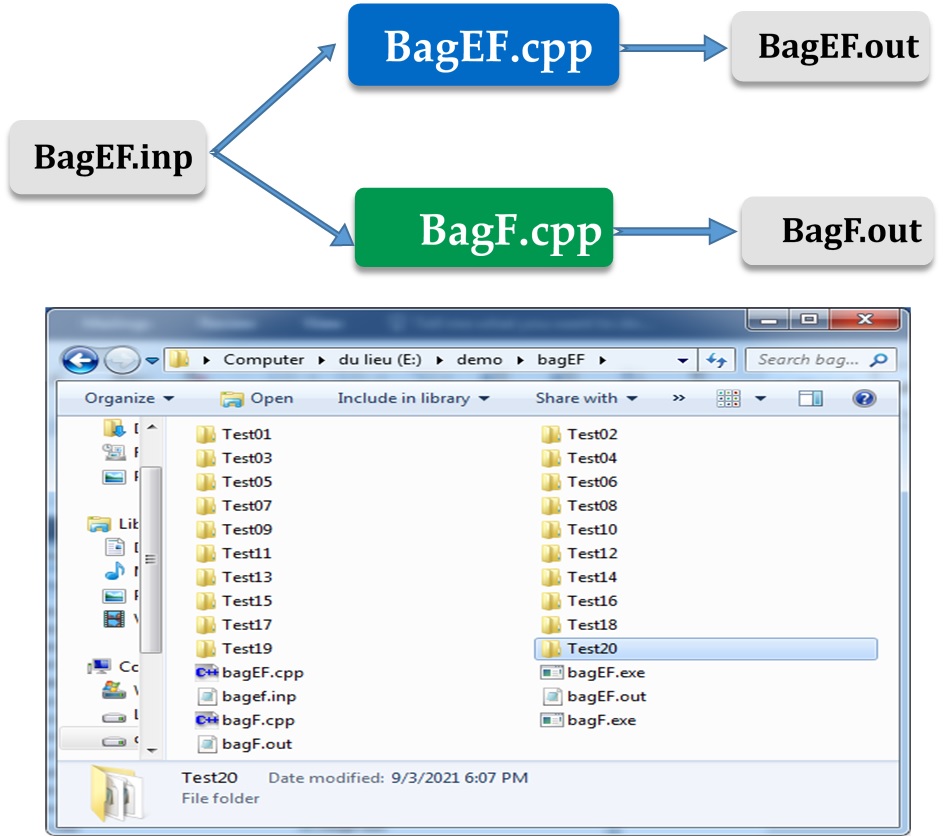
Để tham khảo thêm các tệp chương trình nguồn, các bộ Test để so sánh, đối chiếu các bạn có thể truy cập vào các đường link sau:

https://www.mediafire.com/folder/53dou40j01n6w/demo

Hoặc   https://drive.google.com/drive/folders/16c9k0zdeQi9mWTHnv_JX01WQbfCbune7?usp=sharing

Bài 2: Mua quà trung thu

Một người mang số tiền là P đồng (P <1000), đến cửa hàng chuyên bán bánh kẹo để mua bánh kẹo cho các cháu thiếu nhi nhân dịp tết trung thu. Hiện tại cửa hàng có bày bán n loại bánh kẹo khác nhau (n <1000) có giá lần lượt là: c1,c2,…,cn. Tuy nhiên mỗi loại bánh kẹo, người đó chỉ mua 1 gói. Hãy giúp người đó dùng số tiền của mình một cách hiệu quả nhất theo nghĩa: Số gói kẹo mua được là nhiều nhất nhưng số tiền bỏ ra để mua không được vượt quá P đồng, trong các phương án cùng có số gói kẹo nhiều nhất thì chọn phương án mà số tiền còn lại là ít nhất (lý tưởng nhất là còn 0 đồng)

Dữ liệu vào: là tệp trungthu.inp, có cấu trúc như sau

-         Dòng 1: Hai số nguyen dương n, P

-         Dòng 2: Gồm n số nguyên dương c1,c2,…,cn (ci<1000 với 1≤ i ≤n)

Dữ liệu ra:  Ghi ra tệp trungthu.out

-         Dòng 1: Ghi số gói kẹo nhiều nhất có thể mua

-         Dòng 2: Ghi số tiền dùng để mua

-         Dòng 3: Chỉ số của mỗi loại kẹo được chọn, các số được viết cách nhau bởi dấu cách

(Phương án: Mua 3 gói kẹo thứ 2, 3, 4 là không hiệu quả, vì số tiền còn lại là: 6 đồng)

* Ý tưởng

Bài này cũng là một biến thể của bài toán cái túi. Tuy nhiên ở đây yêu cầu của bài toán là phải đáp ứng được cả 2 tiêu chí. Tiêu chí 1 là: mua được nhiều gói kẹo nhất và không vượt quá P đồng. Tiêu chí 2 là: Nếu có nhiều phương án thỏa mãn tiêu chí 1 thì cần chọn ra được 1 phương án tốt nhất trong các phương án đó (số tiền còn lại là ít nhất)

- Với tiêu chí 1, ta xây dựng hàm mục tiêu F[i][j] như sau:

+ Nếu không chọn gói thứ i thì F[i][j] là giá trị lớn nhất có thể chọn trong số các gói kẹo {1,2,…,i-1} với giới hạn chưa vượt quá số tiền j, tức là:      F[i][j] = F[i-1][j].

+  Nếu có chọn gói thứ i (phải thỏa điều kiện c[i] ≤ j) thì F[i[j] bằng 1 cộng với giá trị lớn nhất có thể có được bằng cách chọn trong số các gói {1,2,…,i-1} với giới hạn số tiền  j-c[i] tức là về mặt giá trị thu được:      F[i][j] = 1 + F[[i-1][j-c[i]]

- Với tiêu chí 2: Là phụ thuộc vào tiêu chí 1. Nghĩa là, khi mà việc chọn gói kẹo thứ i hay không chọn thì giá trị của F[i][j] vẫn không thay đổi, lúc đó ta mới đi xét hàm mục tiêu thứ 2, E[i][j] nếu gói thứ i thỏa mãn cả 2 điều kiện sau thì sẽ chọn gói thứ i

          + c[i] ≤ j

          + E[i-1][j-c[i]]+c[i]> E[i][j]  ( Nghĩa là về mặt số lượng, số gói kẹo vẫn không thay đổi nhưng số tiền cần bỏ ra để mua thì nhiều hơn)

Vậy trước hết, ta có thể khởi tạo giá trị cho bảng phương án như sau:

   fill(F[0],F[0]+nmax*nmax,0);

    fill(E[0],E[0]+nmax*nmax,0);

III. Kết luận

Trong bài viết này, tôi đã trình bày cách sử dụng kết hợp 2 hàm mục tiêu một lúc để giải các bài toán thuộc dạng bài toán cái túi nên đã giúp cho việc giải các bài toán dạng này được tối ưu hơn. Hy vọng rằng, với việc bổ sung 1 số câu lệnh trong thuật toán cái túi (ở đây mới chỉ sử cùng lúc 2 hàm mục tiêu như đã đề cập ở 2 bài toán trên, những bài toán phức tạp hơn ta có thể tăng lên sử dụng 3 hoặc 4 hàm mục tiêu….) thì thuật toán cái túi  sẽ có nhiều ứng dụng hơn trong học tập đồng thời cũng được sử dụng thiết thực hơn trong thực tế nhằm góp phần tiết kiệm chi phí, tăng lãi suất trong sản xuất, kinh doanh

Vì kinh nghiệm và kiến thức của người viết còn có nhiều hạn chế nên lời trình bày có thể  chưa được rõ ràng, cô đọng,… mong được sự đóng góp ý kiến từ phía người đọc

Nguyễn Văn Thống 

(Giáo viên Trường THPT Nguyễn Công Trứ, huyện Nghi Xuân - Hà Tĩnh)

Email: thongnv2005@gmail.com